Κοιτώντας τα διαγράμματα επιδημιολογικής εξέλιξης του κορονοιού σε αρκετές χώρες, παρατηρούμε ότι τείνουν να διαμορφώσουν μία καμπύλη σχήματος S. Αυτή η καμπύλη ονομάζεται σιγμοειδής στα ελληνικά και logistics curve στα εγγλέζικα. Είναι πολύ γνωστή διότι εμφανίζεται σε ποικίλα διάφορα φαινόμενα και μάλιστα υπάρχουν ήδη αρκετοί μαθηματικοί τύποι 3 τουλάχιστον παραμέτρων, που μπορούν να την αναπαράγουν. Αυτές οι παράμετροι είναι χαρακτηριστικές και καθορίζουν αν η καμπύλη θα είναι συμπιεσμένη ή στρετσαρισμένη κατά την οριζόντια διάσταση ή την κατακόρυφη διάσταση.
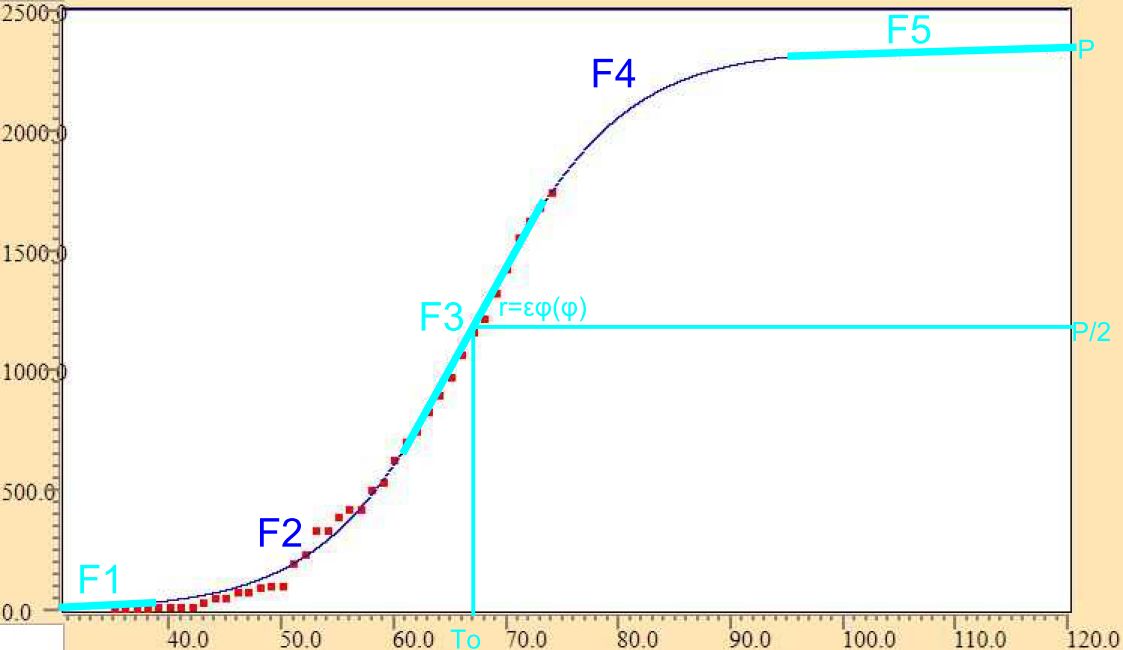
Η σιγμοειδής καμπύλη Π(t) = P / ( 1 + exp( -r ( t - To ) )
Επιλέξαμε την λογιστική - σιγμοειδή καμπύλη Π(t) = P / ( 1 + exp( -r ( t - To ) ), διότι είναι ημιεμπειρική, δηλαδή προκύπτει από θεωρητικό μοντέλο πληθυσμιακής αύξησης, οι 3 παράμετροί της όμως απαιτούν πειραματικά δεδομένα για να προσδιοριστούν.
Αυτή η καμπύλη προκύπτει από την διαφορική εξίσωση dΠ / dt = r Π ( 1 - Π / P ), η οποία μας λέει ότι ο ρυθμός της πληθυσμιακής μεταβολής dΠ / dt ως προς τον χρόνο εξαρτάται από την ειδική ταχύτητα r, την τιμή του πληθυσμού Π και τον μειωτικό παράγοντα 1 - Π / P. Για μικρές τιμές του πληθυσμού στην αρχή του φαινομένου η ταχύτητα εξέλιξης είναι ασθενώς αυξανόμενη εκθετικά, διότι εξαρτάται κυρίως από τον παράγοντα Π. Για μεγάλες τιμές του πληθυσμού προς το τέλος του φαινομένου η ταχύτητα εξέλιξης είναι ασθενώς μειούμενη εκθετικά, διότι εξαρτάται κυρίως από τον παράγοντα 1 - Π / P. Για μεσαίες τιμές του πληθυσμού, προς το μέσον της εξέλιξης του φαινομένου, η ταχύτητα εξέλιξης είναι σταθερή και ισχυρά υψηλή.
Αυτά περιγράφονται και γεωμετρικά στις φάσεις F του σχήματος:
- αρχική εκθετική αύξηση F1F2
- αργή γραμμική φάση F1
- γρήγορη εκθετική φάση F2
- μέγιστη σταθερή αύξηση F3
- τελική εκθετική αύξηση F4F5
- γρήγορη εκθετική φάση F4
- αργή γραμμική φάση F5
Παρατηρώντας το σχήμα:
- το P εκφράζει την τιμή σταθεροποίησης του πληθυσμού μετά από αρκετό χρόνο
- το r εκφράζει την κλίση ανόδου της εκρηκτικής φάσης F3
- το To εκφράζει την χρονική στιγμή που η ταχύτητα αυξησης του πληθυσμού γίνεται η μέγιστη (σημείο καμπής)
- το To επίσης εκφράζει την χρονική στιγμή που ο πληθυσμός φτάνει στο 50% της τελικής του τιμής
Η προσαρμογή της καμπύλης στα δεδομένα
Όπως προαναφέραμε, οι τιμές των P, r και To μπορούν να προσδιοριστούν μόνο όταν υπάρχουν διαθέσιμα πειραματικά δεδομένα. Αυτά τα δεδομένα χρησιμοποιούνται ώστε να προκύψει εκείνη η καμπύλη που θα απέχει τις μικρότερες δυνατές αποστάσεις από τα πειραματικά σημεία (ελάχιστα τετράγωνα). Η υλοποίηση αυτής της εργασίας γίνεται με μη γραμμικούς επαναληπτικούς αλγόριθμους που βασίζονται σε μεθοδολογία των Levenberg-Marquardt. Αυτή την μεθοδολογία εφαρμόσαμε στην καμπύλη του σχήματος για τα δεδομένα της χώρας μας μέχρι και την 05-04-2020. Οι βέλτιστες τιμές των παραμέτρων της καμπύλης που περιγράφει τα δεδομένα στις 05-04-2020 είναι P=2336 άτομα, r=0.1513/ημέρα, To=67 ημέρες.
Η αξία του r έγκειται στην σύγκριση των καμπυλών διαφορετικών χωρών και όσο πιο μεγάλη είναι η τιμή του τόσο πιο εκρηκτικός είναι ο ρυθμός εμφάνισης καταγεγραμμένων κρουσμάτων.
Από το Το αντιλαμβανόμαστε ότι έχει παρέλθει η 67η ημέρα, που παρατηρήθηκε ο μέγιστος ρυθμός αύξησης κρουσμάτων, και ήδη βρισκόμαστε στην φάση της μείωσης του ρυθμού εμφάνισης (βρισκόμαστε στην 74η ημέρα).
Το P μας λέει ότι τα συνολικά καταγεγραμμένα κρούσματα δεν θα ξεπεράσουν τα 2336.
Εδώ όμως πρέπει να κρατούμε μικρό καλάθι διότι το μοντέλο κάνει τις προβλέψεις του για πειραματικά δεδομένα που δεν φαίνεται ξεκάθαρα να έχουν περάσει τουλάχιστον στην φάση F4. Δια του λόγου αυτού η πιο ευαίσθητη παράμετρος είναι η Ρ. Η υψηλή ευαισθησία - χαμηλή αξιοπιστία της πρόβλεψης για το Ρ φαίνεται αν πάμε κάθε φορά μία μέρα πίσω και ξαναυπολογίσουμε την καμπύλη για τα δεδομένα εκείνης της ημέρας.
| t | Π | Πfit | P |
| 35 | 1 | 18.2 | |
| 36 | 3 | 21.2 | |
| 37 | 4 | 24.6 | |
| 38 | 4 | 28.6 | |
| 39 | 7 | 33.2 | |
| 40 | 7 | 38.5 | |
| 41 | 7 | 44.7 | |
| 42 | 9 | 51.8 | |
| 43 | 31 | 60.1 | |
| 44 | 45 | 69.6 | |
| 45 | 46 | 80.6 | |
| 46 | 73 | 93.2 | |
| 47 | 73 | 107.7 | |
| 48 | 89 | 124.4 | |
| 49 | 99 | 143.5 | |
| 50 | 99 | 165.3 | |
| 51 | 190 | 190.1 | |
| 52 | 228 | 218.2 | |
| 53 | 331 | 250.1 | |
| 54 | 331 | 285.9 | 1336.8 |
| 55 | 387 | 326.1 | 770.4 |
| 56 | 418 | 370.9 | 619.4 |
| 57 | 418 | 420.6 | 524.7 |
| 58 | 495 | 475.3 | 564.7 |
| 59 | 530 | 535.2 | 598.2 |
| 60 | 624 | 600.2 | 713.8 |
| 61 | 695 | 670.1 | 862.9 |
| 62 | 743 | 744.6 | 962.4 |
| 63 | 821 | 823.4 | 1086.7 |
| 64 | 892 | 905.8 | 1202.8 |
| 65 | 966 | 991.0 | 1313.2 |
| 66 | 1061 | 1078.1 | 1463.6 |
| 67 | 1156 | 1166.3 | 1634.0 |
| 68 | 1212 | 1254.5 | 1708.6 |
| 69 | 1314 | 1341.7 | 1829.5 |
| 70 | 1415 | 1427.0 | 1970.7 |
| 71 | 1544 | 1509.5 | 2183.4 |
| 72 | 1613 | 1588.4 | 2297.4 |
| 73 | 1673 | 1663.1 | 2331.1 |
| 74 | 1735 | 1733.2 | 2335.9 |
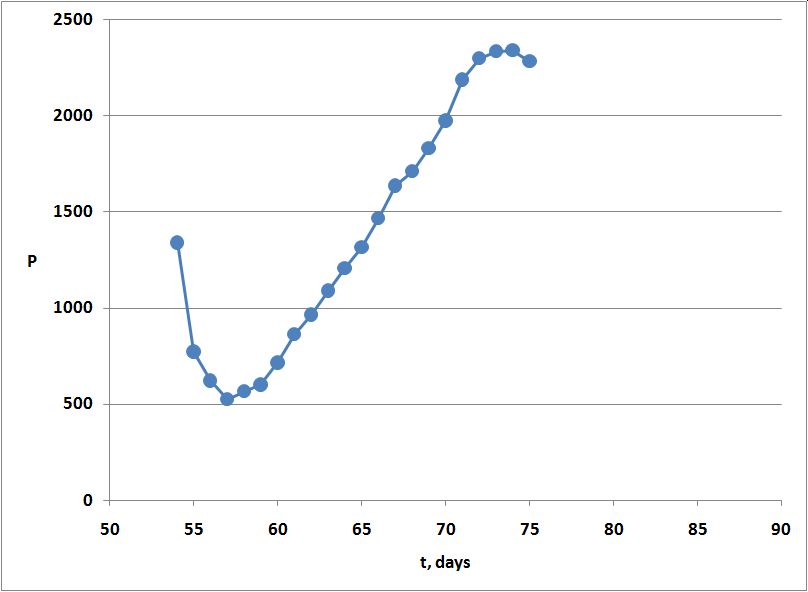
Εφαρμόσαμε αυτή την διαδικασία από την 54η ημέρα (16-03-2020) μέχρι και την 74η (06-04-2020). Τα δεδομένα από την 53η ημέρα και πίσω δεν επαρκούν ώστε το μοντέλο να μπορεί να δώσει μια λογικά αποδεκτή τιμή. Οι υπολογισμένες τιμές του P για κάθε ημέρα δίνονται στον προηγούμενο πίνακα. απεικονίζονται στο πιο κάτω διάγραμμα και δείχνουν για την ώρα μία τάση σταθεροποίησης στην περιοχή του 2300. Αναμένουμε τα δεδομένα των επόμενων ημερών για να δούμε αν θα αλλάξει κάτι. Επιπλέον, δεν πρέπει να ξεχνάμε ότι αυτά είναι μόνο τα καταγεγραμμένα συμβάντα, πόσα άραγε είναι όλα τα πραγματικά συμβάντα σε επίπεδο χώρας? Εκτιμούμε τουλάχιστον μία ή το πολύ δύο τάξεις μεγέθους περισσότερα, δηλαδή κάπου μεταξύ 23.000 - 230.000 συμβάντα.
.
Διάβασε επίσης:.
Η Kemioteko Engineering δημιουργήθηκε ως απόσταγμα εμπειριών 14 ετών στην αδειοδότηση, κατασκευή και λειτουργία δημόσιων τεχνικών έργων και 8 ετών στο ελεύθερο επάγγελμα του μελετητή μηχανικού με εξειδίκευση στην αδειοδότηση και λειτουργία επιχειρήσεων. Αποστολή της Kemioteko Engineering - Χατζηλιόντος Ι. Χριστόδουλος είναι η δημιουργία πελατών, οπαδών της, βαθειά ικανοποιημένων, που θέλουν να κάνουν διαχρονικά τα σωστά πράγματα με τους κατάλληλους συνεργάτες.
Μητρώο Αξιολογητών ΓΓΕΤ- No 14856/95711/08-06-17